Brain, cognition, and teaching 3

Teaching can be an isolated profession. It is why I do this blog: more for my own desire to communicate the things I think through on a daily basis, rather than for fame or money. I think that perhaps the most effective professional development, in dollars for benefit, is simply to pay teachers of the same subject to sit down and talk about the curriculum and instruction, with no explicit goal except sharing ideas. The keys to quality teaching are: to have the teacher think through how to order the concepts in a subject in a way that reasonably challenge the students and to think about ways to set up the classroom such that students do the thinking for themselves. No more, no less.

I have mentioned that I think there are three key characteristics of a good lesson plan or of a good curriculum:

1. it is set up to help students retain key facts and ideas;
2. it is set up to engage students in thinking conceptually about what they are doing, so in other words, the lesson plan or curriculum is set up to make sure students have an abstract understanding of the key facts and ideas;
3. it is set up to give students opportunities to develop general mathematical skills, such as estimating, problem-solving, proof-writing, etc.

These are the "buy a spice rack" ideas. In my last post in this series, I discussed the structuring of review problems, specifically by varying the contexts in which the concepts are presented. In this post, I discuss the second and third characteristics.

Abstraction

The second characteristic is really about abstraction, and one could think of Bloom's taxonomy. A modified version for mathematics is:

• the student can recognize a pattern
• the students can use the pattern
• the students can see the limits to the pattern
• the students can formulate the pattern clearly in their own words
• the students can understand why the pattern works
• the students can offer a solid proof of why the pattern works

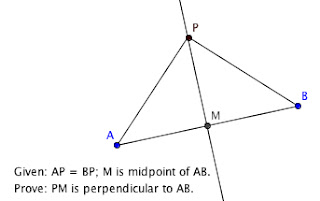
Let's take a particular idea from geometry, that the points on a perpendicular bisector are always equidistant from the endpoints of the bisected segment, through the list:

• Stage "Observe": Students are given a perpendicular bisector line and asked to measure the distance AP and BP and recognize the distances are equal.
• Stage "Apply": When asked to find a point equidistant between A and B, students construct a perpendicular bisector.
• Stage "Limitations": Students recognize that this is NOT the same thing as finding a point equal distance from two lines.
• Stage "Theorem stating": Students can say, "Every point on a perpendicular bisector are equidistant from the endpoints of the bisected segment," or, "The perpendicular bisector is the set of all points equidistant from the endpoints of the bisected segment."
• Stage "Understanding": While their understanding may be idiosyncratic, the key is recognizing that all the points P are the vertices of isosceles triangles. I think the best description I have read of insight is from Why Don't Children Like School?: an insight comes from recognizing two ideas, already understood, are related. The example the author uses is hitting a car and a baseball with a baseball bat; we know what will happen, and the connection is realizing that the force = mass x acceleration equation tells us the car will not move nearly as much as the baseball.
• Stage "Proof": Students can write a proof, usually by showing through congruent triangles that an isosceles triangle's median line is perpendicular to its base.

It is impossible to proceed into further abstraction without a solid grasp of the more concrete stages. Now, it would be ideal for students to progress all the way on every concept, but that is not necessarily possible. Advanced classes can push to the more abstract levels; mid-level classes might stop half-way through. Advanced class should NOT go through more material faster at only a middle level of abstraction. Sadly, however, many math classes -- even advanced classes -- probably stop at the application stage. Students simply do problems, but they are never asked about how all the pieces of math fit together. For all but the very weakest students, this is a loss.

Now, I hear a lot of people talk about how important it is for students to do proofs in geometry, but I think in many geometry courses, the proofs just get tacked on at the end, and the students do not have a satisfactory grasp of the earlier stages of a concept they are being asked to prove. It is better that they be asked to think at a reasonably challenging level of abstraction, and this will vary from concept to concept. For the perpendicular bisector theorem, the "understanding" stage is attainable for most students, so it is not unreasonable to do a proof. For other ideas, such as the idea that the perpendicular bisectors of the sides of the triangle meet at its circumcenter, I would expect students to stall out at the "theorem stating" stage, so a proof of this concept is out of reach. (Yes, I know the concepts are logically almost the same, but I find the complexity of working with three lines begins to overwhelm them, and it really is unattainable.)

In mathematics, sometimes the simplest ideas are the hardest to understand. Here are some topics I have found that my classes stall out at the "theorem stating" stage:

- Distance = A - B; and if B is a negative number, then the distance = A + absolute value (B).
- A radical is actually a length that can be plotted and manipulated.
- The edge of a circle is a set of points.
- A line is a set of points.

Even though my classes will not prove these concepts, that does not make the concepts any less worthwhile. Proofs are good where appropriate, but they are not the only way to induce students to think abstractly about the mathematical interconnections. Questions like, "Will the pattern work here?," "State this idea in your own words," and "Explain why..." demand a more thoughtful approach than plug-and-chug, especially when the teacher holds the students to high standards. A fantastic example of very abstract thinking, requiring no proofs, is to ask students to categorize quadrilaterals into "families" based on shared properties.

Problem-solving

The third characteristic of a good curriculum is that it gives students the opportunity to develop mathematical skills, such as number sense, estimation, and problem-solving. I think they are all important skills, but problem-solving is the most crucial in many ways. Here is my attempt to provide some vocabulary to describe good problems for practice.


First, how similar to problems the students have already seen is a problem? You can call any work in math "problem-solving," but it only really counts if the problems are novel.

Second, how many concepts do students need to pull together to solve a problem? This is the heart of problem-solving: realizing you can use a hammer and nails and a saw and a drill to make a birdhouse.

Third, how divergent are the concepts? If the students must put together a concept from geometry with another one from calculus, it is more challenging.

Fourth, how salient are the concepts? If it obvious that the triangle inequality is used to solve a problem, then this is a high salience concept. Does the problem have false leads? Does it tempt students to do X when Y is right? (Closely related to salience is how recently a concept was learned or reviewed.)

Fifth, how far must students go down a path before they can see it is right? As students practice problem-solving, their perseverance goes up, but a lot of students begin the year convinced that if a problem takes more than two steps, they must be doing it wrong.

Sixth, how difficult are the concepts? There is the question to of what students need to do with the concept. If the method requires students to use the contra positive of a known theorem, it can cause some students to nearly melt down. The converse thoroughly baffles expectations. One of my favorite arguments as a debater was, "Causality works the other direction." I would concede that there was a link between X and Y, but that, contrary to my opponent's assertion that X caused Y, it was actually Y that caused X. This caused endless difficulty for them to answer; few people could explain the causal mechanism well enough to rebut this tactic.

Seventh, how much algebra must the students do? How much translation from words to pictures or equations, or from pictures to equations? Every act of translating from one representation to another increases the complexity.


The key question is the mental load students are under to solve a problem. How many pieces are floating around, how well they understand those pieces (very familiar or still novel), the complexity of combination and operations they must do -- all these elements combine to make problems more challenging. And this is the key distinction between a regular and advanced-track student: the more advanced student is capable of making larger logical jumps to connect two ideas, of dealing with larger gaps in explanations of concepts (not struggling to move to more abstract ideas, not having difficulty moving beyond the details of concrete examples), and of seeing/remembering/using more complex patterns (seeing all the nuances and exceptions; inferring how to navigate contrapositives, converses, and inverses fluidly).