Triangle incenters for Pythagorean triples

For any triangle, the incenter is the center of the largest circle that will fit inside the triangle, like so:

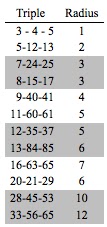
A Pythagorean triple is a right triangle with whole number sides, such as a 3-4-5 triangle. I found by accident that the radius of the incircle is always a whole number, too (not a fact listed on Wikipedia but listed on Wolfram MathWorld). There is an additional element to the pattern.

Here is the first dozen Pythagorean triples, by length of shortest side. As you can see, as the shortest side gets longer, the incircle radius does, too, although this pattern is not consistent.

It turns out that every Pythagorean triple (a, b, c) can be written in the form

where r and s are any two positive integers such that r > s. So the chart can be amended to this (side a in bold italics):

Then I swapped rows 9 and 10 to make the pattern clearer:

The key was recognizing that the quantity r - s is meaningful:

As is clear, the radius is s * (r - s). Now to go about proving it. Let's start by creating a generic Pythagorean triple right triangle, like this:

The method for finding the incenter is easy: find the point of intersection of the angle bisectors. The angle bisector of the right angle is easy: y = x. To find a second angle bisector, use the angle bisector ratio property that the angle bisector divides the third side like so,

where

.

So, in our Pythagorean triple triangle, the angle bisector sets up the ratio

.

Therefore, the angle bisector passes through the point

and has the equation

.

The solution to the two equations -- the point of intersection -- is therefore

.

This confirms the result from the table. Since both r and s were integers to begin with, s * (r - s) is also an integer. Every Pythagorean triple right triangle has an integer incircle radius, as well.

Bonus method!

One neat property of the incircle (for all triangles) is that the area of the triangle is equal to 0.5 (incircle radius) * perimeter. Observe:

D, the center of the incircle, is equidistant from sides AB, AC, and BC. Radius DE is the shortest distance to side AC, and therefore forms a right angle and is an altitude to triangle ACD. The area of ACD is 0.5 (incircle radius) * AC. Likewise for triangle BCD: the area is 0.5 (incircle radius) * BC. And for triangle ABD: the area is 0.5 (incircle radius) * AB. Since ABD, ACD, and BCD cover all of ABC, the area of triangle ABC is 0.5 (incircle radius) * (AB + AC + BC).

On any Pythagorean triple triangle, we know:

and also:

Given our property for the incircle on any triangle, we know:

Therefore:

which confirms what we found before!